Question

Tiffany has $4,000 andsaves $50 per month. Sarah's savings baland after x months is modeled by the function f(x) = 3,000(1.01)*. If Tiffany and Sarah begin saving at the same time, after approximately how many months will the balances of their savings be the same?

Answer 1

The balances of their savings will be the same approximately after 122 months

Explanation:

Let

x ----> the number of months

f(x) ----> Sarah's savings balance

g(x) ---> Tiffany's savings balance

we know that

Tiffany's savings balance

The function g(x) is a linear function

The function g(x) in slope intercept form is equal to

`g(x)=50x+4,000`

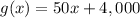
Sarah's savings balance

The function f(x) is a exponential growth function

The function f(x) is equal to

`f(x)=3,000(1.01)^x`

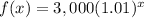
Solve the system by graphing

Remember that the solution of the system of equations is the intersection point both graphs

using a graphing tool

The solution is the point (122,10,099.83)

see the attached figure

therefore

The balances of their savings will be the same approximately after 122 months