Question

The heating coil of a hot water heater has a resistance of 17 Ω and operates at 300 V. How long a time is required to raise the temperature of 115 kg of water from 18°C to 75°C? (The specific heat for water = 10 3 cal/kg ⋅°C and 1.0 cal = 4.186 J).

Answer 1

5183 sec.

Step-by-step explanation:

• The power dissipated in the resistance, will be used to raise the temperature of the water completely.
• This power can be found applying Joule's law, which states the following:

`P = I^(2)*R (1)`

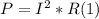
• If the resistance of the heating coil can be assumed as constant with the temperature, we can find the current I applying Ohm's Law, as follows:

`I = (V)/(R) = (300V)/(17 \Omega) = 17.7 A`

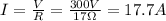
• Now, from (1) we can find P, as follows:

`P = I^(2) * R = (17.7A)^(2) * 17 \Omega = 5294.1 J/s`

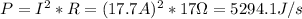
• The energy supplied by this power, is just the product of the power times the time during which the energy was delivered:

`E = P* \Delta t (2)`

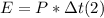
• This energy, will be supplied as heat to the mass of water, as stated by the following equation (assuming no heat losses out of the heater):

`\Delta Q = c*m*\Delta T (3)`

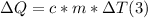
• where c= specific heat of water = 4186 J/ºC*kg, m= 115 kg, and ΔT= 57ºC.
• From (2) and (3), if left sides are equal each other, so do right sides:

`P* \Delta t = c*m*\Delta T`

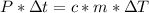
• Replacing by the values, we can solve for Δt, as follows:

`\Delta t = (c*m*\Delta T)/(P) = (4186 J/deg*kg*115 kg*57 deg)/(5294.1J/s) \\ \Delta t = 5183 sec.`

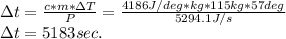
• The time required to raise the temperature of 115 kg of water, from 18ºC, to 75ºC, is 5183 sec (approximately 1hr 26').