Answer:
(a) The probability that someone will test positive and have HIV is 0.000025.
(b) The probability that someone will test positive and not have HIV is 0.0001.
(c) The probability that someone will test positive is 0.000125.
(d) The probability a person has HIV given that he/she was tested positive is 0.1986.
Explanation:
Denote the events as follows:
X = a person has HIV
Y = a person is tested positive for HIV.
The information provided is:
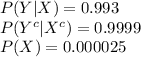
Compute the probability of a person not having HIV as follows:
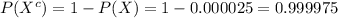
Compute the probability of
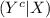 as follows:
as follows:
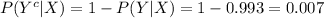
Compute the probability of as
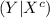 follows:
follows:
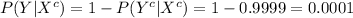
(a)
Compute the probability that someone will test positive and have HIV as follows:
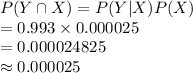
Thus, the probability that someone will test positive and have HIV is 0.000025.
(b)
Compute the probability that someone will test positive and not have HIV as follows:
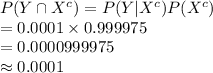
Thus, the probability that someone will test positive and not have HIV is 0.0001.
(c)
Compute the probability that someone will test positive as follows:
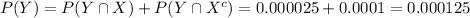
Thus, the probability that someone will test positive is 0.000125.
(d)
Compute the probability a person has HIV given that he/she was tested positive as follows:
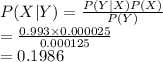
Thus, the probability a person has HIV given that he/she was tested positive is 0.1986.
As the probability of a person having HIV given that he was tested positive is not very large, it would not be wise to implement a random testing policy.