Question

Use the Pohlig–Hellman algorithm (Theorem 2.32) to solve the discrete logarithm problem gx = a in Fp in each of the following cases.(a) p = 433, g = 7, a = 166.(b) p = 746497, g = 10, a = 243278.(c) p = 41022299, g = 2, a = 39183497. (Hint. p =2·295 + 1.)(d) p = 1291799, g = 17, a = 192988. (Hint. p−1 has a factor of 709.)

Answer 1

(a) The solution is x=47.

(b) The solution is x=223755.

(c) The solution is x=33703314.

(d) The solution is x=984414.

Explanation:

(a) Step 1 is to solve

q e
`h = g^( (p-1)) /q`
`b = a^((p-1)) /q`
`h^(y) = b`

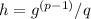
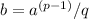
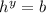
2 4 265 250 Calculation I

3 3 374 335 Calculation II

Now Solving for calculation I:

x≡
`x_(0) +x_(1) q+…+x_(e-1) q^(e-1) (mod\ 2^(4) )`≡
`0x_(0)+2x_(1) +4x_(2) +8x_(3) (mod\ 2^(4) )`

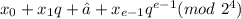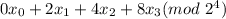
Solve (265)x=250(mod 433) for x0,x1,x2,x3.

x0:(26523)x0=25023(mod 433)⟹(432)x0=432⟹x0=1

x1:(26523)x1=(250×265−x0)22(mod 433)=(250×265−1)22(mod433)=(250×250)22(mod 433)⟹(432)x1=432⟹x1=1

x2:(26523)x2=(250×265−x0−2x1)21(mod 433)=(250×265−3)22(mod 433)=(250×195)21(mod 433)⟹(432)x2=432⟹x2=1

x3:(26523)x3=(250×265−x0−2x1−4x2)20(mod 433)=(250×265−7)20(mod 433)=(250×168)20(mod 433)⟹(432)x3=432⟹x3=1

Thus, our first result is:

x≡x0+2x1+4x2+8x3(mod24)≡1+2+4+8(mod24)≡15(mod24)

Now for Calculation II:

x≡
`x_(0) +x_(1) q+…+x_(e-1) q^(e-1) (mod\ 3^(3) )`≡
`x_(0)*0+3x_(1) +9x_(2) (mod3^(3))`

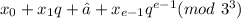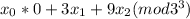
Solve (374)x=335(mod 433) for x0,x1,x2.

x0:(37432)x0=33532(mod 433)⟹(234)x0=198⟹x0=2. Note: you only needed to test x0=0,1,2, so it is clear which one x0 is.

x1:(37432)x1=(335×374−x0)31(mod 433)=(335×374−2)31(mod 433)=(335×51)31(mod 433)=1(mod 433)⟹(234)x1=1(mod 433)⟹x1=0

x2:(37432)x2=(335×374−x0−3x1)30(mod 433)=(335×374−2)30(mod 433)=(335×51)30(mod 433)=198(mod 433)⟹(234)x2=198(mod 433)⟹x2=2. Note: you only needed to test x2=0,1,2, so it is clear which one x2 is.

Thus, our second result is:

x≡x0+3x1+9x2(mod 33)≡2+0+9×2(mod 33)≡20(mod 33)

Step 2 is to solve

x ≡15 (mod 24 ),

x ≡20 (mod 33 ).

The solution is x=47.

(b) Step 1 is to solve

q e
`h = g^( (p-1)) /q`
`b = a^((p-1)) /q`
`h^(y) = b`

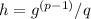
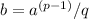
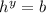
2 10 4168 38277 523

3 6 674719 322735 681

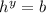`h^(y) = b` is calculated using same steps as in part(a).

Step 2 is to solve

x ≡ 523 (mod 210 ),

x ≡ 681 (mod 36 ).

The solution is x=223755 .

(c) Step 1 is to solve

q e
`h = g^( (p-1)) /q`
`b = a^((p-1)) /q`
`h^(y) = b`

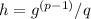
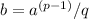
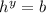
2 1 41022298 1 0

29 5 4 11844727 13192165

In order to solve the discrete logarithm problem modulo 295 , it is best to solve it step by step. Note that 429 = 18794375 is an element of order 29 in F∗p . To avoid notational confusion, we use the letter u for the exponents.

¢294

First solve 18794375u0 = 11844727

= 987085.

The solution is u0 = 7.

The value of u so far is u = 7.

¢293

Solve 18794375u1 = 11844727·4−7

= 8303208.

The solution is u1 = 8.

The value of u so far is u = 239 = 7 + 8 · 29.

¢292

Solve 18794375u2 = 11844727 · 4−239

= 30789520.

The solution is

u2 = 26. The value of u so far is u = 22105 = 7 + 8 · 29 + 26 · 292 .

¢291

Solve 18794375u3 = 11844727 · 4−22105

= 585477.

The solution is

u3 = 18. The value of u so far is u = 461107 = 7 + 8 · 29 + 26 · 292 + 18 · 293 .

¢290

Solve 18794375u4 = 11844727 · 4−461107

= 585477.

The solution is

u4 = 18. The final value of u is u = 13192165 = 7 + 8 · 29 + 26 · 292 + 18 · 293 + 18 · 294 , which is the number you see in the last column of the table.

Step 2 is to solve

x ≡ 13192165 (mod 295 ).

x ≡ 0 (mod 2),

The solution is x=33703314 .

(d) Step 1 is to solve

q e
`h = g^( (p-1)) /q`
`b = a^((p-1)) /q`
`h^(y) = b`

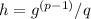
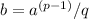
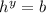
2 1 1291798 1 0

709 1 679773 566657 322

911 1 329472 898549 534

To solve the DLP’s modulo 709 or 911, they can be easily solved by an exhaustive search on a computer, and a collision algorithm is even faster.

Step 2 is to solve

x ≡ 0 (mod 2),

x ≡ 322 (mod 709),

x ≡ 534 (mod 911).

The solution is x=984414