Answer:
The phase difference between these two waves is 141.1⁰
Step-by-step explanation:
The displacement of the wave is given as;
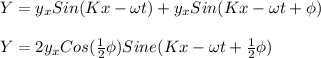
Amplitude, A = 2yₓCos(¹/₂Φ)
Since the amplitude of the combination is 1.5 times that of one of the original amplitudes = yₓ = 1.5 × A = 1.5A
A = 2(1.5A)Cos(¹/₂Φ)
A = 3ACos(¹/₂Φ)
¹/₃ = Cos(¹/₂Φ)
(¹/₂Φ) = Cos ⁻(0.3333)
(¹/₂Φ) = 70.55°
Φ = 141.1°
The phase difference between these two waves is 141.1⁰