Answer:
Statements (1) and (2) TOGETHER are NOT sufficient.
Explanation:
If y ≠ 1, is x = 1 ?
(1)
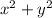 = 1
= 1
(2) y = 1 – x
The two statements are not sufficient to assert this claim. The statement If y ≠ 1, is x = 1 only holds in the two statements if y=0 as seen below.
(1)
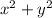 = 1
= 1
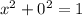
x=1
(2) y = 1 – x
0=1-x
x=1
Every other value of y fails the condition. So a sufficient statement would have been:
If y ≠ 1, and y=0, is x = 1 ?
(1)
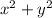 = 1
= 1
(2) y = 1 – x