Question

What is the maximum number of lines per centimeter a diffraction grating can have and produce a complete first-order spectrum for visible light? Assume visible light has a range of 400 nm to 700 nm.

Answer 1

14,300 lines per cm

Step-by-step explanation:

Answer:

14,300 cm per line

Step-by-step explanation:

λ400 nm to 400nm

We can find the maximum number of lines per centimeter, which is reciprocal of the least distance separating two adjacent slits, using the following equation.

mλ = dsin (θ)

In this equation,

m is the order of diffraction.

λ is the wavelength of the incident light.

d is the distance separating the centers of the two slits.

θ is the angle at which the mth order would diffract.

To find the least separation that allows the observation of one complete order of spectrum of the visible region, we use the maximum wavelength of the visible region is 700 nm.

d = mλ / sin (θ)

As we want the distance d to be the smallest then sin (θ) must be the greatest, and the greatest value of the sin (θ) is 1. For that we also use the longest wavelength because using the smallest wavelength, the longest wavelength would not be diffracted.

d = mλ / sin (θ)

d = 1 x 700nm / 1

= 700 nm

So, the least separation that would allow for the possibility of observing complete first order of the visible region spectra is 700 nm, and knowing the least separation we can find the maximum number of lines per cm, which is the reciprocal of the number of lines per cm.

n = 1/d

= 1 / 700 x
`10^(-9)`

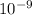
= 1, 430,000 lines per m

= 14,300 lines per cm

The maximum number of lines per cm, that would allow for the observation of the complete first order visible spectra.