Question

The following is the frequency distribution for the speed of a sample of automobiles traveling on an interstate highway. Speed (mph) Frequency 50 - 54 4 55 - 59 3 60 - 64 2 65 - 69 5 70 - 74 2 75 - 79 5 The standard deviation is ______.

Answer 1

Standard Deviation is 18.57 .

Explanation:

We are given the frequency distribution for the speed of a sample of automobiles traveling on an interstate highway;

Speed (mph) Frequency (f) X X*f X -
`Xbar`
`(X-Xbar)^(2)`

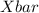
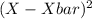
50 - 54 4 52 208 52 - 65 = -13 169

55 - 59 3 57 171 57 - 65 = -8 64

60 - 64 2 62 124 62 - 65 = -3 9

65 - 69 5 67 335 67 - 65 = 2 4

70 - 74 2 72 144 72 - 65 = 7 49

75 - 79 5 77 385 77 - 65 = 12 144

∑f = 21 ∑X*f = 1367

Mean of the data,
`Xbar` =
`(\sum Xf)/(\sum f)`

=
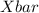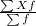
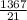`(1367)/(21)` = 65.09 ≈ 65 .

Now, Standard deviation, s =
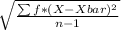
`\sqrt{(\sum f*(X-Xbar)^(2) )/(n-1)}`

s =
`\sqrt{((4*169)+(3*64)+(2*9)+(5*4)+(2*49)+(5*144))/(6-1) }` =
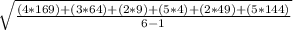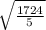`\sqrt{(1724)/(5) }` = 18.57

Therefore, standard deviation is 18.57 .