Question

Which procedure justifies whether -3x(5-4)+3(x-6) is equivalent to -12x-6?

The expressions are not equivalent because -3(2)(5-4) +3(2-6)=-18 and -12(2)-6--30
The expressions are not equivalent because -3(2)(5-4)+ 3(2-6) --18 and -12(3)-6=-42
The expressions are equivalent because -3(2)(5-4)+3(2-6)=-18 and -12(-2)-6-18
The expressions are equivalent because -3(2)(5-4)+ 3(2-6)=-18 and -12(1)-6--18

Answer 1

Option (a) is correct.

Explanation:

Given : Expressions 3x(5-4)+3(x-6) and -12x-6

We have to choose which option from the given options justifies the correct procedure to show the given two expressions are equivalent or not.

Since to check two given expressions are equivalent or not. Simply put the same value of unknown and evaluate the values of both the given expressions. If it comes out to be the same then they are equivalent otherwise not.

Consider the given expression 3x(5-4)+3(x-6) and -12x-6

Evaluate both at x = 2

So, 3(2)(5-4)+3(2-6) = -18

and -12(2)-6 = -30

So both the expressions are not equivalent.

Hence, option (a) is correct.

Answer 2

Explanation:

Equivalent Expressions

One approach that can be followed to know if two expressions are equivalent is to evaluate them for the same value of the independent value. If by chance they are equal for that value, it doesn't prove they are equivalent, but if they are not equal, then we can infer they are NOT equivalent.

Let's analyze these expressions

`-3x(5-4)+3(x-6) \ ,\ -12x-6`

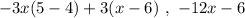
We'll use the value x=2:

`-3\cdot 2(5-4)+3(2-6) \ ,\ -12\cdot 2-6`

`-12 \ ,\ -30`

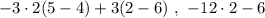
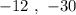
This result matches the first option provided in the question. For the sake of completeness, we'll check the other options.

`-3(2)(5-4)+ 3(2-6) =-18 \ ,\ -12(3)-6=-42`

The above statement is true, but the second result is obtained for a different value of x respect to the first result. So it does not qualify as a valid proof.

We'll simplify the first expression

`-3x(5-4)+3(x-6) =-3x(1)+3x-18=-18`

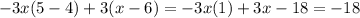
The result is not equivalent to -12x-6. Thus, the two other options are false.