Question

You are on the market for a new car. You want to check whether there is a significant difference between the fuel economy of mid-size domestic cars and mid-size import cars. You sample 17 domestic car makes and find an average fuel economy of 34.904 MPG with a standard deviation of 4.6729 MPG. For imports, you sample 15 cars and find an average MPG of 28.563 MPG with a standard deviation of 8.4988. Construct a 90% confidence interval for the difference between the true average fuel economies in question. Assume the difference will represent (domestic - import). You can also assume that the standard deviations are statistically the same between the two populations.

Answer 1

Explanation:

Hello!

The objective is to test if there is a difference between the fuel economy of mid-size domestic cars and mid-size import cars.

For this there are two samples taken:

X₁: Fuel economy of a domestic car.

Sample 1

n₁= 17 domestic cars

X[bar]₁= 34.904 MPG

S₁= 4.6729 MPG

X₂: Fuel economy of an import car.

Sample 2

n₂= 15 import cars

X[bar]₂= 28.563 MPG

S₂= 8.4988 MPG

To estimate the difference between the average economic fuel of domestic cars and import cars, assuming both variables have a normal distribution and both population variances are unknown but equal, the statistic to use is a t-test for two independent samples with pooled sample variance:

(X[bar]₁-X[bar]₂)±
`t_(n_1+n_2-2;1-\alpha /2) * (Sa*\sqrt{(1)/(n_1) +(1)/(n_2) } )`

`Sa^2= ((n_1-1)S_1^2+(n_2-1)S^2_2)/(n_1+n_2-2)`

`Sa^2= (16*(4.6729)^2+14*(8.4988)^2_2)/(17+15-2)= 45.35`

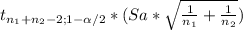
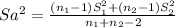
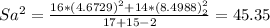
Sa= 6.73

`t_(n_1+n_2-2;1-\alpha /2) = t_(30; 0.95)= 1.697`

(34.904-28.563)±
`1.697* (6.73*\sqrt{(1)/(17) +(1)/(15) } )`

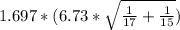
6.341±1.697*2.38

[2.30;10.38]

With a confidence level of 90%, you'd expect that the difference between the average economic fuel of domestic cars and import cars will be contained in the interval [2.30;10.38].

I hope it helps!