Answer:
![[2,4]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/wjmk063k3mblgpbuy42ngn8yiszdnaatd0.png)
Explanation:
On a coordinate plane, a curved line has minimum values of (negative 1.56, negative 6) and (3, 0). This means
1) when
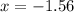 , the minimum value of the function is
, the minimum value of the function is
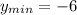
2) when
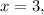 the minimum value of the function is
the minimum value of the function is

Hence, the graphed function has a local minimum of 0, when

Therefore, the interval which contains this value of x is
![[2,4]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/wjmk063k3mblgpbuy42ngn8yiszdnaatd0.png) because
because
![x=3\in [2,4].](https://img.qammunity.org/2021/formulas/mathematics/middle-school/98we80i3o0971w2u1jtvs0hcmz0vplbg54.png)