Answer:
The z score for bolt of diameter 18.12 mm is 1.20.
Explanation:
Let X = diameter of bolts.
It is provided that the random variable X follows a Normal distribution with mean, μ = 18 mm and standard deviation, σ = 0.10 mm.
A z-score is a standardized score, a numerical, that defines how far a data value from the mean.
The distribution of z-scores is defined by the Standard Normal distribution.
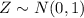
The formula to compute the z-score is:

The value of the diameter of a bolt is, x = 18.12 mm.
Compute the z-score for this value as follows:
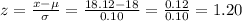
Thus, the z score for bolt of diameter 18.12 mm is 1.20.