Question

A 1.5-mm layer of paint is applied to one side of the following surface. Find the approximate volume of paint needed. Assume that x and y are measured in meters. The spherical zone generated when the curve y = Squareroot 42x - x^2 on the interval [1, 6] is revolved about the x-axis. The volume of paint needed is __________m^3. (Type an exact answer, using pi as needed.)

Answer 1

210π m^3

Explanation:

Area of surface of revolution about the x axis =
`\int\limits^p_q {2\pi y(x)√(1 + y'(x)^2) } \, dx \\\\`

`y(x) =√(42x-x^2) \\\\y'(x) =((1)/(2)( 42-2x))/(√(42x-x^2) ) \\\\y'(x) =(21-x)/(√(42x-x^2) )`

Area of surface of revolution about the x axis =

`\int\limits^p_q {2\pi y(x)√(1 + y'(x)^2) } \, dx \\\\=\int\limits^6_1 {2\pi * √(42x-x^2)\sqrt{1 + ((21-x)/(√(42x-x^2) ))^2} } \, dx =\int\limits^6_1 {2\pi * √(42x-x^2)\sqrt{ ((42x-x^2 + (21-x)^2)/(42x-x^2 ))} } \, dx\\\\=\int\limits^6_1 {2\pi * \sqrt{ ({42x-x^2 + 441-42x+x^2 })} } \, dx\\\\=\int\limits^6_1 {2\pi * √( 441 ) } \, dx\\\\=\int\limits^6_1 {2\pi * 21 } \, dx\\\\ =42\pi (6-1) = 210\pi`

Answer 2

V = 63π / 200 m^3

Explanation:

Given:

- The function y = f(x) is revolved around the x-axis over the interval [1,6] to form a spherical surface:

y = √(42*x - x^2)

- The surface is coated with paint with uniform layer thickness t = 1.5 mm

Find:

The volume of paint needed

Solution:

- Let f be a non-negative function with a continuous first derivative on the interval [1,6]. The Area of surface generated when y = f(x) is revolved around x-axis over the interval [1,6] is:

`S = 2*\pi \int\limits^a_b { [f(x)*√(1 + f'(x)^2) }] \, dx`

- The derivative of the function f'(x) is as follows:

`f'(x) = (21-x)/(√(42x-x^2) )`

- The square of derivative of f(x) is:

`f'(x)^2 = ((21-x)^2)/(42x-x^2 )`

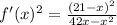
- Now use the surface area formula:

- The Volume of the pain coating is:

V = S*t

V = 210*π*3/2000

V = 63π / 200 m^3