Question

A block is given a very brief push up a 20.0 degree frictionless incline to give it an initial speed of 12.0 m/s.(a) How far along the surface of the plane does the block slide before coming to rest?(b) How much time does it take to return to its starting position?

Answer 1

Step-by-step explanation:

(a) Net force acting on the block is as follows.

`F_(net) = -mg Sin (\theta)`

or, ma = -mg Sin (\theta)[/tex]

a =
`-g Sin (\theta)`

=
`-9.8 * Sin (20^(o))`

= -3.35
`m/s^(2)`

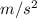
According to the kinematic equation of motion,

`v^(2) - v^(2)_(o) = 2as`

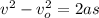
Distance traveled by the block before stopping is as follows.

s =
`(v^(2) - v^(2)_(o))/(2a)`

=
`((0)^(2) - (12.0)^(2)_(o))/(2 * -3.35)`

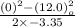
= 21.5 m

According to the kinematic equation of motion,

v =
`v_(o) + at`

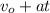
0 =
`12.0 m/s + (1)/(2) * -3.35 m/s^(2) * t`

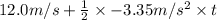
`t_(1)` = 7.16 sec

Therefore, before coming to rest the surface of the plane will slide the box till 7.16 sec.

(b) When the block is moving down the inline then net force acting on the block is as follows.

`F_(net) = -mg Sin (\theta)`

ma =
`mg Sin (\theta)`

a =
`g Sin (\theta)`

=
`9.8 m/s^(2) * Sin (20^(o))`

= 3.35
`m/s^(2)`

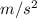
Kinematics equation of the motion is as follows.

s =
`v_(o)t + (1)/(2)at^(2)`

21.5 m =
`0 + (1)/(2) * 3.35 m/s^(2) * t^(2)`

`t_(2)` =
`\sqrt{(2 * 21.5 m)/(3.35 m/s^(2))}`

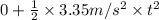
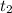= 3.58 sec

Hence, total time taken by the block to return to its starting position is as follows.

t =
`t_(1) + t_(2)`

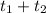
= 7.16 sec + 3.58 sec

= 10.7 sec

Thus, we can conclude that 10.7 sec time it take to return to its starting position.