Answer:
(a). The average force exerted by the wall on him is 406.25 N.
(b). The work done by the wall on him is zero.
(c). The change in the kinetic energy of his center of mass is 203.1 J.
Step-by-step explanation:
Given that,
Mass of ice = 65 kg
Distance = 0.50 m
Speed = 2.5 m/s
(a). We need to calculate the average force exerted by the wall on him
Using work energy theorem
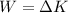
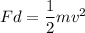
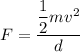
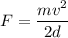
Put the value into the formula
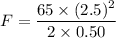

(b). The wall does not move so the displacement is zero.
We need to calculate the work done by the wall on him
Using formula of work done
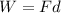
Put the value into the formula
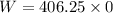
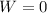
(c). We need to calculate the change in the kinetic energy of his center of mass
Using formula of change in kinetic energy
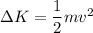
Put the value into the formula
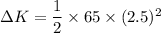
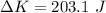
Hence, (a). The average force exerted by the wall on him is 406.25 N.
(b). The work done by the wall on him is zero.
(c). The change in the kinetic energy of his center of mass is 203.1 J.