Question

The College Board reports that 2% of students who take the SAT each year receive special accommodations because of documented disabilities. Consider a random sample of 25 students who have recently taken the test.

a. What is the probability that exactly 1 received a special accommodation?
b. What is the probability that at least 1 received a special accommodation?
c. What is the probability that at least 2 received a special accommodation?
d. What is the probability that the number among the 25 who received a special accommodation is within 2 standard deviations of the number you would expect to be accommodated?
e. Suppose that a student who does not receive a special accommodation is allowed 3 h for the exam, whereas an accommodated student is allowed 4.5 h. What would you expect the average time allowed the 25 selected students to be?

Answer 1

The solution the the given problem is given below.

Explanation:

We have p = P(a student received a special accommodation) = 0.02,

so with X = the number among the 25 who received a special accommodation, X ∼ Bin(25, 0.02).

a) The probability that exactly 1 received a special accommodation is :

P(X = 1) =

`(0.02)^(1)`
`(1-0.02)^(25-1)` = 25(0.02)(0.098)
`^(24)` ≈ 0.3079

b) The probability that at least 1 received a special accommodation is:

P(X ≥ 1) = 1 − P(X = 0) = 1 − (0.98)25 ≈ 1 − 0.6035 = 0.3965

c) The probability that at least 2 received a special accommodation is :

P(X ≥ 2) = 1 − P(X = 0) − P(X = 1) ≈ 1 − 0.6035 − 0.3079 = 0.0886

d) The mean and the standard deviation of X are:

µ = E(X) = np = 25(0.02) = 0.5,

σ =
`√(V(X))` =
`√(np(1-p))` =
`√(25(0.02)(0.98))` =
`√(0.49)` = 0.7

Then, the probability that the number among the 25 who received a special accommodation is within 2 standard deviations of the expected number is :

P(|X − µ| ≤ 2σ) = P(X ≤ µ + 2σ) = P(X ≤ 0.5 + (2)(0.7)) = P(X ≤ 1.9)

= P(X = 0) + P(X = 1) ≈ 0.6035 + 0.3079 = 0.9114.

e) The average time allowed the 25 selected students will be:

`((.5*4.5)+(24.5*3))/(25)` = 3.03 hours.

Answer 2

(a) P(X=1) = 0.3079

(b) P(X≥1) = 0.3965

(c) P(X≥2) = 0.0886

(d) P(X≤1.9) = 0.9114

(e) Expected no. of hours = 3.594 hours

Explanation:

We have,

p = 0.02

n = 25

q = 1-p

q = 0.98

We will use the binomial distribution formula to solve this question. The formula is:

P(X=x) = ⁿCₓ pˣ qⁿ⁻ˣ

where n = total no. of trials

x = no. of successful trials

p = probability of success

q = probability of failure

Let X be the number of students who received a special accommodation.

(a) P(X=1) = ²⁵C₁ (0.02)¹ (0.98)²⁵⁻¹

= 25*0.02*0.61578

P(X=1) = 0.3079

(b) P(X≥1) = 1 - P(X<1)

= 1 - P(X=0)

= 1 - (²⁵C₀ (0.02)⁰ (0.98)²⁵⁻⁰)

= 1 - 0.6035

P(X≥1) = 0.3965

(c) P(X≥2) = 1 - P(X<2)

= 1 - [P(X=0) + P(X=1)]

= 1 - (0.6035 + 0.3079)

= 1 - 0.9114

P(X≥2) = 0.0886

(d) The probability that the number among 25 who received a special accommodation is within 2 standard deviations of the expected number of accommodations. This means we need to compute the probability P(X-μ≤2σ). For this we need to calculate the mean and standard deviation of this distribution.

μ = np = (25)*(0.02) = 0.5

σ =
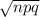`√(npq)` = √(25)*(0.02)*(0.98) = √0.49 = 0.7

P(X-μ≤2σ) = P(X - 0.5≤ 2(0.7)) = P(X≤ 1.4 + 0.5) = P(X≤1.9)

P(X≤1.9) = P(X=0) + P(X=1)

= 0.6035 + 0.3079

P(X≤1.9) = 0.9114

(e) Student who does not receive a special accommodation i.e. X=0 is given 3 hours for the exam whereas an accommodated student P(X>0) is given 4.5 hours. The expected average number of hours given on the exam can be calculated as:

Expected no. of hours = ∑x*P(x)

= 3*P(X=0) + 4.5*P(X>0)

= 3*0.6035 + 4.5(1 - P(X≤0))

= 1.8105 + 4.5(1 - 0.6035)

= 1.8105 + 1.78425

Expected no. of hours = 3.594 hours