Question

From each corner of a square piece of sheet metal 18 centimeters on a side, remove a small square and turn up the edges to form an open box. What should be the dimension of the box so as to maximize its volume?

Answer 1

Height = 3 cm, Length = 9 cm, Width = 9 cm

Explanation:

A square piece of sheet of side x centimeters is cut from the square sheet. When it was folded to make the box the height of box becomes x, length becomes (18-2x) and the width becomes (18-2x).

Volume is given by

`V = Length* Width* Height\\V = (18 - 2x)^2x = x(4x^2-72x+324) = 4x^3-72x^2+324x\\So,\\V(x) = 4x^3-72x^2+324x`

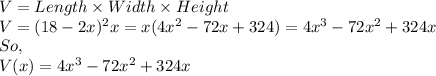
First, we differentiate V(x) with respect to x, to get,

`(d(V(x)))/(dx) = (d(4x^3-72x^2+324x))/(dx) = 12x^2 - 144x +324`

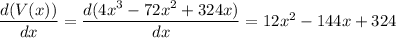
Equating the first derivative to zero, we get,

`(d(V(x)))/(dx) = 0\\\\12x^2 - 144x +324 = 0`

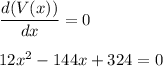
Solving, with the help of quadratic formula, we get,

`x =9,x=3`

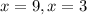
Again differentiation V(x), with resopect to x, we get,

`(d^2(V(x)))/(dx^2) = 24x - 144`

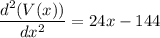
At x = 9

`(d^2(V(x)))/(dx^2) > 0`

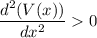
At x = 3

`(d^2(V(x)))/(dx^2) < 0`

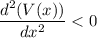
Thus, by double differentiation test, the maxima occurs at x = 3 for V(x).

Thus, largest volume the box can have occurs when x = 3.

Dimensions of box:

Height = x = 3 cm

Length = (18-2x) = 9 cm

Width = (18-2x) = 9 cm