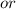 The general equation that represents height of the t-shirt as a function of time:
The general equation that represents height of the t-shirt as a function of time:
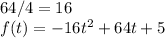
The maximum height of the t-shirt:
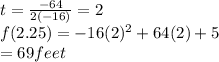
How long will it take the t-shirt to reach its maximum height:
2 seconds
How long does it take for the t-shirt to reach the crowd:
![49=-16t^(2) +69t+5\\o=-16t^(2)+69t-30\\\\\frac{-64+\sqrt[]{-64^(2-4(-16)(-30))} }{2(-16)} = .54](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ju51ffr0pipnlt3vlur1zt8cuwjuqv5w7g.png)
 or
or
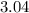
The range of this graph in inequality and interval notation:
![heights(y)\\5\leq y\leq 69 [5,86]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/lj8fgdleulayn0s9q1wiyxkgpa54yzvcok.png)