Question

Using the right triangle below, find the cosine of angle A.

Answer 1

Angle A = 36.87°.

Solution:

Given data:

The side opposite to angle A is a.

The side opposite to angle B is b.

The side opposite to angle C is c.

a = 6, b = 8, c = 10

Using law of cosine:

`a^(2)=b^(2)+c^(2)-2 b c \cos A`

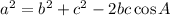
Substitute the given values in the formula,

`6^(2)=8^(2)+10^(2)-2* 8 * 10 \cos A`

`36=64+100-160 \cos A`

`36=164-160 \cos A`

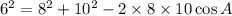
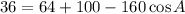
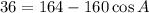
Subtract 164 from both sides of the equation.

`-128=-160 \cos A`

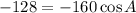
Divide by –160 on both sides of the equation.

`$(-128)/(-160) =(-160 )/(-160 ) \cos A`

`$(4)/(5) =\cos A`

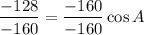
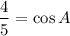
Switch the sides.

`$\cos A=(4)/(5)`

`$ A=\cos^(-1)\left((4)/(5)\right)`

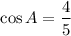
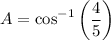
A = 36.87°

Hence angle A = 36.87°.