Answer:
The velocity is 1003.5 m/s and the acceleration is 103.1 m/
 .
.
Step-by-step explanation:
We need to find the parameter equation of x. To find it, we will need to integrate the x-component acceleration equation given to us, twice. Acceleration is:
a =
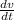
dv = adt
∫dv = ∫adt
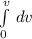 =
=
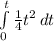
v =
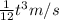 .
.
Velocity is:
v =
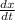
dx=vdt
Again, integrate both sides:
∫dx = ∫vdt
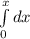 =
=
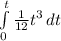
x =
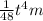
Substitute our x equation into our parameter equation of y.
y
 = [120(
= [120(
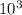 )x] m
)x] m
y
 = [120(
= [120(
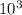 )(
)(
 )(
)(
 ) ]
) ]
(take the square root of both sides and simplify)
y = 50

Now that we can represent our equation with respect to time, we can take the derivative to figure out the velocity. Remember that taking the derivative of a position function gives us the velocity function.
y = 50

vy= y = 100t
Let us write down the two equations for velocity we found:
vx =
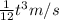
vy = 100t m/s
At t = 10 s:
vx =
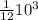 = 83.3 m/s
= 83.3 m/s
vy = 100(10)=1000 m/s
The magnitude of velocity is:
v =
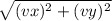
v =
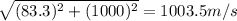
To figure out the acceleration, we need to figure out ay which can be found by taking the derivative of the vy equation,
vy = 100t m/s
ay = vy = 100 m/

Since ax is given to us in the question, we have the following:
ax =

ay = 100 m/

At t = 10 s:
ax =
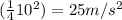
ay = 100 m/

The magnitude of acceleration is equal to:
a =
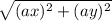
a =

a= 103.1 m/

Final Answers:
v = 1003.5 m/s
a= 103.1 m/
