Answer:
Option A.
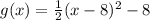
Explanation:
The complete question is
The function g is given in three equivalent forms.
Which form most quickly reveals the vertex?
A)g(x)= 1/2(x-8)^2-8
B)g(x)= 1/2(x-12)(x-4)
C)g(x)= 1/2x^2-8x+24
we know that
The equation of a quadratic function in vertex form is equal to

where
a is the leading coefficient
(h,k) is the vertex of the function
In this problem, the option A is the equation of the function in vertex form
we have
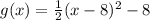
where the vertex is the point (8,-8)
therefore
Option A