Answer:
The number of turns in the solenoid is 230.
Step-by-step explanation:
Given that,
Rate of change of current,
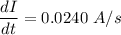
Induced emf,
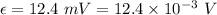
Current, I = 1.5 A
Magnetic flux,
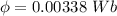
The induced emf through the solenoid is given by :
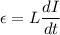
or
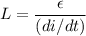 ........(1)
........(1)
The self inductance of the solenoid is given by :
 .........(2)
.........(2)
From equation (1) and (2) we get :
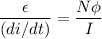
N is the number of turns in the solenoid

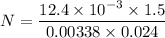
N = 229.28 turns
or
N = 230 turns
So, the number of turns in the solenoid is 230. Hence, this is the required solution.