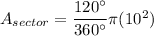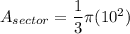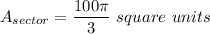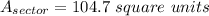Question

Please help I only have 10 minutes left to submit this (:

Find the area of each sector. Show your work.

Answer 1

`A_(sector) = (100\pi)/(3)`

`A_(sector) = 104.7 ~square~units`

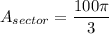
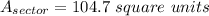
Explanation:

The area of a full circle is

`A = \pi r^2`

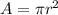
A full circle has a central angle of 360 degrees.

The area of a sector is a fraction of the area of a full circle and is proportional to the central angle of the sector.

For a sector:

`A_(sector) = (n)/(360^\circ)\pi r^2`

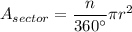
where n = central angle of sector.

Here you have a radius of 10 and a central angle of 120 deg.

`A_(sector) = (120^\circ)/(360^\circ)\pi(10^2)`

`A_(sector) = (1)/(3)\pi(10^2)`

`A_(sector) = (100\pi)/(3) ~square~units`

`A_(sector) = 104.7 ~square~units`