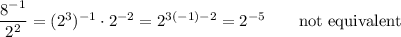Question

Select all the expressions that are equivalent

Answer 1

B, C, D

Explanation:

One of the rules of exponents is that an exponent in the numerator is equivalent to the opposite of the same exponent in the denominator. That means ...

`4^(-3)=(1)/(4^3)\qquad\text{matches C.}`

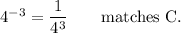
Another rule of exponents is that an exponent represents repeated multiplication. If a factor can be written using an exponent, the exponents are effectively multiplied.

`4^(-3)=(2^2)^(-3)=2^(2(-3))=2^(-6)\qquad\text{matches B.}`

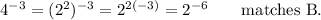
Of course, that repeated multiplication can be shown explicitly:

`(1)/(4^3)=(1)/(4)\cdot(1)/(4)\cdot(1)/(4)\qquad\text{matches D.}`

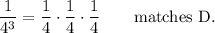
The equivalent expressions to 4^(-3) are B, C, D.

_____

Additional comment

The expression of G evaluates to ...

`(8^(-1))/(2^2)=(2^3)^(-1)\cdot2^(-2)=2^(3(-1)-2)=2^(-5)\qquad\text{not equivalent}`