Answer:
FIRST ANNUITY
The accumulated Value =
![P[((1+r)^(n) - 1)/(r)] * (1+r)](https://img.qammunity.org/2021/formulas/business/college/kti7ntsf9hegnn92bd6d6u1zfok3mi4wd5.png)
The accumulated Value =
![21.80[((1.109)^(n) - 1)/(0.109)] * (1.109)](https://img.qammunity.org/2021/formulas/business/college/m2mz9cdgxyp6pu5kcf4dglo36y0vhc7o7n.png)
SECOND CASH-FLOW
We can simply calculate our answer by evaluating the perpetuity as no variable is missing. Hence,
The Present Value =
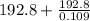
The Present Value = 192.8 + 1768.8
The Present Value = 1961.61
As per the question :
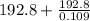 =
=
![21.80[((1.109)^(n) - 1)/(0.109)] * (1.109)](https://img.qammunity.org/2021/formulas/business/college/m2mz9cdgxyp6pu5kcf4dglo36y0vhc7o7n.png)
Hence, second expression is also approx equal to $1960.