Question

A particle of mass m moves under an attractive central force F(r) = -Kr4 with angular momentum L. For what energy will the motion be circular, and what is the radius of the circle? Find the frequency of radial oscillations in the particle is given a small radial impulse.

Answer 1

The energy of a particle in circular motion can be determined using the formula E = (1/2)m(v^2 + r^2ω^2). By setting the central force equal to the centripetal force, the radius of the circular motion and the energy of the particle can be found.

Step-by-step explanation:

The energy of a particle in circular motion is given by the formula E = (1/2)m(v^2 + r^2ω^2), where m is the mass of the particle, v is its velocity, r is the radius of the circular motion, and ω is the angular velocity. In this case, the central force is given by F(r) = -Kr^4, and for circular motion, the force must be equal to the centripetal force, which is represented by F = mv^2/r. Setting these equal to each other, we can solve for the radius of the circular motion and the energy of the particle.

Answer 2

Angular velocity is same as frequency of oscillation in this case.

ω =
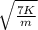`\sqrt{(7K)/(m) }` x
`[(L^(2))/(mK)]^(3/14)`

Step-by-step explanation:

- write the equation F(r) = -K
`r^(4)` with angular momentum L

- Get the necessary centripetal acceleration with radius r₀ and make r₀ the subject.

- Write the energy of the orbit in relative to r = 0, and solve for "E".

- Find the second derivative of effective potential to calculate the frequency of small radial oscillations. This is the effective spring constant.

- Solve for effective potential

- ω =
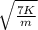`\sqrt{(7K)/(m) }` x
`[(L^(2))/(mK)]^(3/14)`