Question

Fairfield Homes is developing two parcels near Pigeon Fork, Tennessee. In order to test different advertising approaches, it uses different media to reach potential buyers. The mean annual family income for 12 people making inquiries at the first development is $153,000, with a standard deviation of $42,000. A corresponding sample of 24 people at the second development had a mean of $171,000, with a standard deviation of $30,000. Assume the population standard deviations are the same.

1.State the decision rule for .05 significance level: H0: ?1 = ?2; H1:?1 ? ?2. (Negative amounts should be indicated by a minus sign. Round your answers to 3 decimal places.)
Reject H0 if t is not between and .
2.Compute the value of the test statistic. (Negative amount should be indicated by a minus sign. Round your answer to 2 decimal places.)
Value of the test statistic
3.At the .05 significance level, can Fairfield conclude that the population means are different?

Answer 1

(1) Null Hypothesis,
`H_0` :
`\mu_1 = \mu_2`

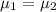
Alternate Hypothesis,
`H_1` :
`\mu_1\\eq \mu_2`

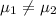
(2) Test statistics = -1.48

(3) At the 0.05 significance level, Fair field conclude that the population means are same.

Explanation:

Let
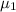`\mu_1` = mean annual family income for 12 people making inquiries at the first development

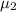`\mu_2` = mean annual family income for 24 people making inquiries at the second development

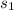`s_1` = standard deviation of annual family income for 12 people making inquiries at the first development

`s_2` = standard deviation of annual family income for 24 people making inquiries at the second development

`n_1` = sample of people of first development i.e. 12

`n_2` = sample of people of second development i.e. 24

(1) Null Hypothesis,
`H_0` :
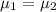`\mu_1 = \mu_2` {population means are same}

Alternate Hypothesis,
`H_1` :
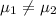`\mu_1\\eq \mu_2` {population means are different}

DECISION RULE ;

• If the test statistics is less than the critical value of t from table at 5% significance level, then we will accept null hypothesis,
  `H_0` .
• If the test statistics is more than the critical value of t from table at 5% significance level, then we will reject null hypothesis,
  `H_0` .

(2) The test statistics is given by;

`\frac{(X_1bar -X_2bar) - (\mu_1-\mu_2)}{s_p\sqrt{(1)/(n_1)+(1)/(n_2) } }` ~
`t_n__1+n_2-2`

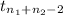
where,
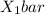`X_1bar` = Sample mean income of people at first development

= $153,000

`X_2bar` = Sample mean income of people at second development = $171,000

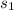`s_1` = $42,000 and
`s_2` = $30,000

`s_p= \sqrt{((n_1-1)s_1^(2)+(n_2-1)s_2^(2) )/(n_1+n_2-2)}` =
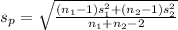`\sqrt{((12-1)42000^(2)+(24-1)30000^(2) )/(12+24-2)}` = 34344.30

Test statistics =
`\frac{(153000 -171000) - 0}{34344.30\sqrt{(1)/(12)+(1)/(24) } }` ~
`t_3_4`

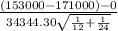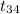
= -1.48

(3) At 5% level of significance, t table gives critical value of 2.032 at 34 degree of freedom.Since our test statistics is less than the critical value of t so considering our decision rule, we will accept null hypothesis.

And conclude that population means are same.