Answer:
The mean return is $9 and the risk is $3.1.
Explanation:
It is provided that on investing an amount of $100 in the two investments the return will be X and Y.
Given:

It is also provided that the investor invested $31 and $69 in the first and second investment respectively.
The return equation will be:
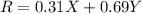
Compute the expected value of return as follows:
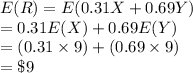
Thus, the mean return is $9.
Compute the risk as follows:
Risk = SD (0.31X + 0.69Y)
 Thus, the risk is $3.1.
Thus, the risk is $3.1.