Answer:
(a) The value of P (X = 7) is 0.1377.
(b) The value of P (X ≥ 3) is 0.9380.
(c) The value of P (2 < X < 7) is 0.5443.
(d) The standard deviation of X is 2.4495
Explanation:
Let X = the number of tracks counted in 1 cm² of surface area.
It is provided that the average number of tracks is 6 per cm².
The random variable
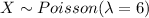 .
.
The probability function of a Poisson distribution is:

(a)
Compute the value of P (X = 7) as follows:
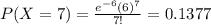
Thus, the value of P (X = 7) is 0.1377.
(b)
Compute the value of P (X ≥ 3) as follows:
P (X ≥ 3) = 1 - P (X < 3)
= 1 - P (X = 0) - P (X = 1) - P (X = 2)
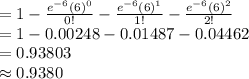
Thus, the value of P (X ≥ 3) is 0.9380.
(c)
Compute the value of P (2 < X < 7) as follows:
P (2 < X < 7) = P (X = 3) + P (X = 4) + P (X = 5) + P (X = 6)
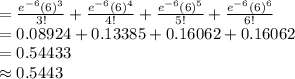
Thus, the value of P (2 < X < 7) is 0.5443.
(d)
The standard deviation of a Poisson distribution is:
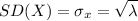
Compute the value of standard deviation of X as follows:
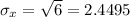
Thus, the standard deviation of X is 2.4495