The time taken by the object to reach the ground is
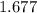 (app.)
(app.)
Step-by-step explanation:
The given function is
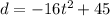
To graph the function in the graph, let us substitute the values for t to find the value of d.
t d
0 45
1 29
2 -19
3 -99
4 -211
5 -355
These values are plotted in the graph which is attached below:
To determine the time it takes the object to reach the ground, let us substitute
 in the function
in the function
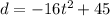 , we get,
, we get,
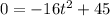
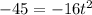
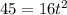
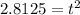

The value of t cannot be negative.
Thus,
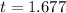 (app.)
(app.)
Thus, the time taken by the object to reach the ground is
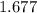 (app.)
(app.)