Question

Let Ab e an invertiblen×nmatrix, and let B be ann×pmatrix. Show thatthe equationAX=Bhas a unique solutionA−1B. Hint: You need to show thatA−1Bis a solution, and that there is no other solution. You might do this secondpart by making an argument each column ofB

Answer 1

In fact,
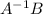`A^(-1) B` is a solution to the equation AX = B. Let me show you.

Explanation:

Step 1 .

Remember that there's a very special
`n`x
`n` matrix, called "the identity matrix", we denote it as
`I_(N)`.

That matrix is special because

`I_(N)`*(Any matrix) = Any matrix,

So, when I say, "Any matrix", that literally means, "Any martrix", well, any
`n`x
`n` matrix. Therefore;

`I_(N)`*A = A

Step 2.

Remember that A is invertible if there exist a matrix
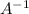`A^(-1)` such that

`A` *
`A^(-1)` =
`I_(N)`.

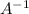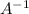`A^(-1)` is just the name of it, the most important is the property I just mentioned.

Step 3.

Now, to show that, we just have to show that
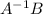`A^(-1) B` is a solution of
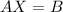`AX = B`, in other words we have to show that,
`A*(A^(-1) B) = B`

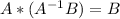
Notice that

`A*(A^(-1) * B ) = (A*A^(-1) ) *B = I_(N) * B = B`

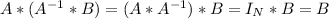
Therefore,
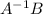`A^(-1) B` is a solution of
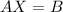`AX = B`.