Question

In IR spectroscopy, we normally talk about "frequencies" when in reality we are referring to wavenumbers. What is the mathematical relationship between frequency and wavenumber? Between wavenumber and wavelength? What are the units most commonly used for frequency, wavelength, and wavenumber?

Answer 1

Here's what I get.

Step-by-step explanation:

(b) Wavenumber and wavelength

The wavenumber is the distance over which a cycle repeats, that is, it is the number of waves in a unit distance.

`\bar \\u = (1)/(\lambda)`

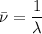
Thus, if λ = 3 µm,

`\bar \\u = \frac{1}{3 * 10^(-6) \text{ m}}= 3.3 * 10^(5)\text{ m}^(-1) = \textbf{3300 cm}^(-1)`

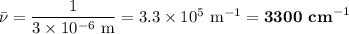
(a) Wavenumber and frequency

Since

λ = c/f and 1/λ = f/c

the relation between wavenumber and frequency is

`\bar \\u = \mathbf{(f)/(c)}`

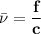
Thus, if f = 90 THz

`\bar \\u = \frac{90 * 10^(12) \text{ s}^(-1)}{3 * 10^(8) \text{ m$\cdot$ s}^(-1)}= 3 * 10^(5) \text{ m}^(-1) = \textbf{3000 cm}^(-1)`

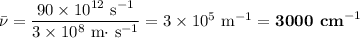
(c) Units

(i) Frequency

The units are s⁻¹ or Hz.

(ii) Wavelength

The SI base unit is metres, but infrared wavelengths are usually measured in micrometres (roughly 2.5 µm to 20 µm).

(iii) Wavenumber

The SI base unit is m⁻¹, but infrared wavenumbers are usually measured in cm⁻¹ (roughly 4000 cm⁻¹ to 500 cm⁻¹).