Answer: The mass of rust that can be removed is 1.597 grams
Step-by-step explanation:
To calculate the number of moles for given molarity, we use the equation:
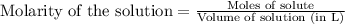 .....(1)
.....(1)
Molarity of oxalic acid solution = 0.1255 M
Volume of solution =
 = 600 mL = 0.600 L (Conversion factor: 1 L = 1000 mL)
= 600 mL = 0.600 L (Conversion factor: 1 L = 1000 mL)
Putting values in equation 1, we get:

For the given chemical reaction:
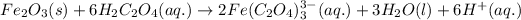
By Stoichiometry of the reaction:
6 moles of oxalic acid reacts with 1 mole of ferric oxide (rust)
So, 0.06 moles of oxalic acid will react with =
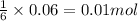 of ferric oxide (rust)
of ferric oxide (rust)
To calculate the mass of rust for given number of moles, we use the equation:
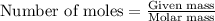
Molar mass of rust (ferric oxide) = 159.7 g/mol
Moles of rust = 0.01 moles
Putting values in above equation, we get:
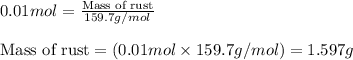
Hence, the mass of rust that can be removed is 1.597 grams