Question

According to the Bureau of Transportation​ Statistics, 81.9​% of American Airlines flights were on time in 2017. Assume this percentage still holds true for American Airlines. For the next 40 flights from American​ Airlines, use the normal approximation to the binomial distribution to complete parts a through d.

a. Determine the probability that fewer than 34 flights will arrive on time.
b. Determine the probability that exactly 32 flights will arrive on time.
c. Determine the probability that 25​, 26​, 27​, or 28 flights will arrive on time.
d. Determine the probability that 28​, 29​, 30​, 31​, or 32 flights will arrive on time.

Answer 1

To solve this problem, we can use the normal approximation to the binomial distribution. The mean (µ) for the number of flights arriving on time out of 40 flights is 32.76 flights. The standard deviation (σ) is 3.58 flights.

Step-by-step explanation:

To solve this problem, we can use the normal approximation to the binomial distribution. The mean (µ) for the number of flights arriving on time out of 40 flights is 40 * 0.819 = 32.76 flights. The standard deviation (σ) is sqrt(40 * 0.819 * (1 - 0.819)) = 3.58 flights.

a. To find the probability that fewer than 34 flights will arrive on time, we need to calculate the z-score for 34 using the formula z = (x - µ) / σ. Then, we can use the z-table or a calculator to find the corresponding probability. The z-score for 34 is (34 - 32.76) / 3.58 = 0.35. The cumulative probability for a z-score of 0.35 is 0.6368. Therefore, the probability that fewer than 34 flights will arrive on time is 0.6368.

b. To find the probability that exactly 32 flights will arrive on time, we can calculate the z-score for 32 and find the corresponding probability. The z-score for 32 is (32 - 32.76) / 3.58 = -0.21. The cumulative probability for a z-score of -0.21 is 0.4168. Therefore, the probability that exactly 32 flights will arrive on time is 0.4168.

c. To find the probability that 25, 26, 27, or 28 flights will arrive on time, we need to calculate the cumulative probabilities for each of these values separately and then sum them up. The cumulative probability for 25 is 0.0074, for 26 is 0.0151, for 27 is 0.0284, and for 28 is 0.0476. Summing up these probabilities, we get 0.0985. Therefore, the probability that 25, 26, 27, or 28 flights will arrive on time is 0.0985.

d. To find the probability that 28, 29, 30, 31, or 32 flights will arrive on time, we need to calculate the cumulative probabilities for each of these values separately and then sum them up. The cumulative probability for 28 is 0.0476, for 29 is 0.0758, for 30 is 0.1136, for 31 is 0.1596, and for 32 is 0.2073. Summing up these probabilities, we get 0.6039. Therefore, the probability that 28, 29, 30, 31, or 32 flights will arrive on time is 0.6039.

Answer 2

a)
`P(X\leq 34)=P((X-\mu)/(\sigma)\leq (34-32.76)/(2.435))=P(Z\leq 0.509)=0.695`

Using the real binomial distribution we can use the following excel code:

"=BINOM.DIST(34,40,0.819,TRUE)"

And we got 0.7554

b)
`P(X=32) = (40C32) (0.819)^(32) (1-0.819)^(40-32) = 0.1488`

c)
`P(25<X\leq 28)=P((25-32.76)/(2.435)<(X-\mu)/(\sigma)< (28-32.76)/(2.435))=P(-3.187<Z< -1.955)=P(Z<-1.955)-P(Z<-3.187) =0.0246`

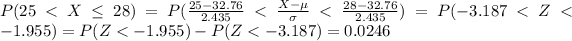
Using the real binomial distribution we can calculate the probability with the following excel formula:

"=BINOM.DIST(28,40,0.819,TRUE)-BINOM.DIST(24,40,0.819,TRUE) "

And we got 0.0453

d)
`P(28<X\leq 32)=P((28-32.76)/(2.435)<(X-\mu)/(\sigma)< (32-32.76)/(2.435))=P(-1.955<Z< -0.312)=P(Z<-0.312)-P(Z<-1.955) =0.3522`

Using the real binomial distribution we can calculate the probability with the following excel formula:

"=BINOM.DIST(32,40,0.819,TRUE)-BINOM.DIST(27,40,0.819,TRUE) "

And we got 0.420

Step-by-step explanation:

Previous concepts

The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".

Let X the random variable of interest, on this case we now that:

`X \sim Binom(n=40, p=0.819)`

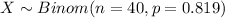
The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

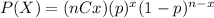
Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

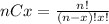
We need to check the conditions in order to use the normal approximation.

`np=40*0.819= 32.76 \geq 10`

`n(1-p)=40*(1-0.819)=7.24`

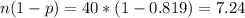
The problem says that we can apply the approximation.

If we appply the approximation the new mean and standard deviation are:

`E(X)=np=40*0.819=32.76`

`\sigma=√(np(1-p))=√(40*0.819(1-0.819))=2.435`

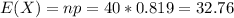
Part a

We want to find this probability:

`P(X\leq 34)`

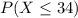
We can use the z score given by this formula
`Z=(x-\mu)/(\sigma)`.

`P(X\leq 34)=P((X-\mu)/(\sigma)\leq (34-32.76)/(2.435))=P(Z\leq 0.509)=0.695`

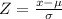Using the real binomial distribution we can use the following excel code:

"=BINOM.DIST(34,40,0.819,TRUE)"

And we got 0.7554

Part b

For this case we want this probability:

`P(X=32)`

We can use the pmf and we got:

`P(X=32) = (40C32) (0.819)^(32) (1-0.819)^(40-32) = 0.1488`

Part c

Since we can use the normal approximation we want to find this probability:

`P(25 < X< 28)`

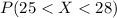
And using the z score formula we got:

`P(25<X\leq 28)=P((25-32.76)/(2.435)<(X-\mu)/(\sigma)< (28-32.76)/(2.435))=P(-3.187<Z< -1.955)=P(Z<-1.955)-P(Z<-3.187) =0.0246`

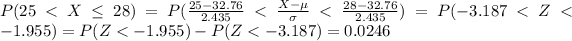
Using the real binomial distribution we can calculate the probability with the following excel formula:

"=BINOM.DIST(28,40,0.819,TRUE)-BINOM.DIST(24,40,0.819,TRUE) "

And we got 0.0453

Part d

`P(28 < X< 32)`

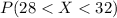
And using the z score formula we got:

`P(28<X\leq 32)=P((28-32.76)/(2.435)<(X-\mu)/(\sigma)< (32-32.76)/(2.435))=P(-1.955<Z< -0.312)=P(Z<-0.312)-P(Z<-1.955) =0.3522`

Using the real binomial distribution we can calculate the probability with the following excel formula:

"=BINOM.DIST(32,40,0.819,TRUE)-BINOM.DIST(27,40,0.819,TRUE) "

And we got 0.420