Question

You own some land at the edge of blacksburg. an individual wants to sign a contract where she rents the land from you for 10 years to operate a golf driving range. she is willing to pay $20,000 per year (at the end of each year). she will then buy the land from you at the end of year 10 for $250,000. alternatively, she is willing to accept a five-year contract, but will only pay $15,000 per year (at the end of each year) and not buy the land at the end of the contract. you suspect that in five years, blacksburg will have grown enough that a developer will buy your land to build new homes. how much does the developer need to pay you at the end of five years to make the shorter contract the better option? assume a 4% interest rate.

Answer 1

Provided the developer offers you more than $321,599.84 in five years, the shorter contract is the better option.

Step-by-step explanation:

We have two options, a ten-year rental and sale or a five-year rental and sale. The problem wants us to figure out how much you need to sell the land for in the five-year case in order to prefer it to the ten-year case. In this setting, we can find the sale price that makes us indifferent, and any amount larger will be preferable.

Step 1: Solve for the PV in the 10-year case.

PV = PV (Rental Annuity) + PV (Sale)

PV = 20000 ×
`[(1)/(r) - (1)/((1+r)^(10)) (1)/(r)] + (250000)/((1.04)^(10) )`

PV = 20000 ×
`[(1)/(0.04) - (1)/((1.04)^(10)) (1)/(0.04)] + (250000)/((1.04)^(10) )`

PV = 20000 × [8.1109] + 168891.04

PV = 162217.92 + 168891.04

PV = $331, 108.96

Step 2: Solve for the five-year sale price that will match the 10-year case PV.

PV = PV (Rental Annuity) + PV (Sale)

331108.96 = 15000 ×
`[(1)/(r) - (1)/((1+r)^(5)) (1)/(r)] + (Sale Price)/((1+r)^(5) )`

331108.96 = 15000 ×
`[(1)/(0.04) - (1)/((1.04)^(5)) (1)/(.04)] + (Sale Price)/((1.04)^(5) )`

331108.96 = 15000 × [4.4518] +
`(Sale Price)/(1.04^(5) )`

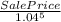
331108.96 = 66777.33 +
`(Sale Price)/(1.04^(5) )`

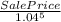
Sale Price = (331108.96 − 66777.33) ×
`1.04^(5)`

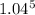
Sale Price = (264331.63) ×
`1.04^(5)`

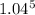
Sale Price = $321, 599.84

Provided the developer offers you more than $321,599.84 in five years, the shorter contract is the better option.