Question

A population of bears increased by 50% in 4 years. If the situation is modeled by an annual growth rate compounded continuously, which formula could be used to find the annual rate according to the exponential growth function?

Answer 1

`A=P(1+(r)/(100) )^n`

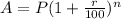
Therefore the annual rate to the exponential growth function is 10.66%

Explanation:

Given that, a population of bears increased by 50% in 4 year.

The growth rate is compound continuously.

So we use the compound formula:

`A=P(1+(r)/(100) )^n`

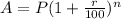
Let the initial population of bear was x.

Since 50% of growth of bear is increased in 4 year.

Therefore the number of bears increased
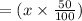`=(x* (50)/(100) )`= 0.5 x in 4 year.

Therefore the total number of bear after 4 years is =(x+0.5x) = 1.5 x

Here A = 1.5x,

P=x,

n=4

Therefore,

`1.5x=x(1+(r)/(100))^4`

`\Rightarrow 1.5=(1+(r)/(100))^4` [ cancel x from both sides]

`\Rightarrow \sqrt[4]{ 1.5}=(1+(r)/(100))`

`\Rightarrow (1+(r)/(100))= 1.1066`

`\Rightarrow (r)/(100)= 1.1066-1`

`\Rightarrow (r)/(100)= 0.1066`

`\Rightarrow r=10.66`

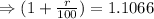
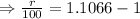
Therefore the annual rate to the exponential growth function is 10.66%.