Question

During a very quick stop, a car decelerates at 7.6 m/s2. Assume the forward motion of the car corresponds to a positive direction for the rotation of the tires (and that they do not slip on the pavement).

(a) What is the angular acceleration of its tires in rad/s2, assuming they have a radius of 0.26 m and do not slip on the pavement?
(b) How many revolutions do the tires make before coming to rest, given their initial angular velocity is 95 rad/s ?

Answer 1

24.57 revolutions

Step-by-step explanation:

(a) If they do not slip on the pavement, then the angular acceleration is

`\alpha = a / r = 7.6 / 0.26 = 29.23 rad/s^2`

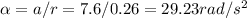
(b) We can use the following equation of motion to find out the angle traveled by the wheel before coming to rest:

`\omega^2 - \omega_0^2 = 2\alpha\Delta \theta`

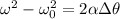
where v = 0 m/s is the final angular velocity of the wheel when it stops,
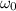`\omega_0` = 95rad/s is the initial angular velocity of the wheel,
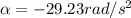`\alpha = -29.23 rad/s^2` is the deceleration of the wheel, and
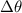`\Delta \theta` is the angle swept in rad, which we care looking for:

`0 - 95^2 = 2*29.23\Delta \theta`

`9025 = 58.46 \Delta \theta`

`\Delta \theta = 9025 / 58.46 = 154.375 rad`

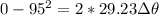
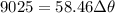
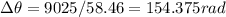
As each revolution equals to 2π, the total revolution it makes before stop is

154.375 / 2π = 24.57 revolutions