Answer:
Thus, the answer is:
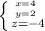
Explanation:
Considering the system of equations
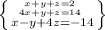
Rewrite the system in matrix form and solve it by Gaussian Elimination (Gauss-Jordan elimination)
![\left \{ {{x+y+z=2} \atop {4x+y+z=14}} \ \atop {x-y+4z=-14}} \right\}\rightarrow \left[\begin{array}{ccc}1&1&1:2\\4&1&1:14\\1&-1&4:-14\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/sc8kbggviuolf0hzxwsr1dxqfv125f6xe4.png)
R2 - 4 R1 → R2 (multiply 1 row by 4 and subtract it from 2 row); R3 - 1 R1 → R3 (multiply 1 row by 1 and subtract it from 3 row)
![\left[\begin{array}{ccc}1&1&1:2\\0&-3&-3:6\\0&-2&3:-16\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/i63uy12k1zqsxnuu1pr73p3xcap5nvw0ys.png)
R2 / -3 → R2 (divide the 2 row by -3)
![\left[\begin{array}{ccc}1&1&1:2\\0&1&1:-2\\0&-2&3:-16\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/syizfp62lllohovti1tqaaoy4j92xioh5f.png)
R1 - 1 R2 → R1 (multiply 2 row by 1 and subtract it from 1 row); R3 + 2 R2 → R3 (multiply 2 row by 2 and add it to 3 row)
![\left[\begin{array}{ccc}1&0&0:4\\0&1&1:-2\\0&0&5:-20\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/jxfj1ugfva55ibvey40xr4hyfiuzd279pp.png)
R3 / 5 → R3 (divide the 3 row by 5)
![\left[\begin{array}{ccc}1&0&0:4\\0&1&1:-2\\0&0&1:-4\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/20oysrzyqcp7x9kn0uf6ziljpca9jn1qh6.png)
R2 - 1 R3 → R2 (multiply 3 row by 1 and subtract it from 2 row)
![\left[\begin{array}{ccc}1&0&0:4\\0&1&0:2\\0&0&1:-4\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/79wtx8yzqd0l3yu1jzq3xhauao94u53fsy.png)
Thus, the answer is:
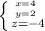
Make a check:
4 + 2 + (-4) = 4 + 2 - 4 = 2
4·4 + 2 + (-4) = 16 + 2 - 4 = 14
4 - 2 + 4·(-4) = 4 - 2 - 16 = -14
Check completed successfully.