Question

Consider the following initial-value problem. (x + y)2 dx + (2xy + x2 − 2) dy = 0, y(1) = 1 Let ∂f ∂x = (x + y)2 = x2 + 2xy + y2. Integrate each term of this partial derivative with respect to x, letting h(y) be an

Answer 1

`(x+y)^2\,\mathrm dx+(2xy+x^2-2)\,\mathrm dy=0`

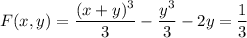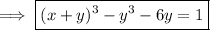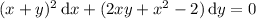
Suppose the ODE has a solution of the form
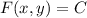`F(x,y)=C`, with total differential

`(\partial F)/(\partial x)\,\mathrm dx+(\partial F)/(\partial y)\,\mathrm dy=0`

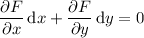
This ODE is exact if the mixed partial derivatives are equal, i.e.

`(\partial^2F)/(\partial y\partial x)=(\partial^2F)/(\partial x\partial y)`

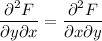
We have

`(\partial F)/(\partial x)=(x+y)^2\implies(\partial^2F)/(\partial y\partial x)=2(x+y)`

`(\partial F)/(\partial y)=2xy+x^2-2\implies(\partial^2F)/(\partial x\partial y)=2y+2x=2(x+y)`

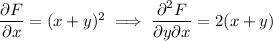
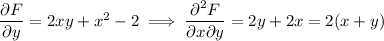
so the ODE is indeed exact.

Integrating both sides of

`(\partial F)/(\partial x)=(x+y)^2`

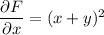
with respect to
`x` gives

`F(x,y)=\frac{(x+y)^3}3+g(y)`

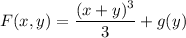
Differentiating both sides with respect to
`y` gives

`(\partial F)/(\partial y)=2xy+x^2-2=(x+y)^2+(\mathrm dg)/(\mathrm dy)`

`\implies x^2+2xy-2=x^2+2xy+y^2+(\mathrm dg)/(\mathrm dy)`

`\implies(\mathrm dg)/(\mathrm dy)=-y^2-2`

`\implies g(y)=-\frac{y^3}3-2y+C`

`\implies F(x,y)=\frac{(x+y)^3}3-\frac{y^3}3-2y+C`

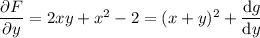
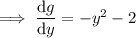
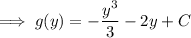
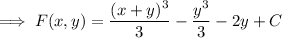
so the general solution to the ODE is

`F(x,y)=\frac{(x+y)^3}3-\frac{y^3}3-2y=C`

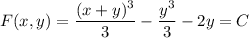
Given that
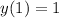`y(1)=1`, we find

`\frac{(1+1)^3}3-\frac{1^3}3-2=C\implies C=\frac13`

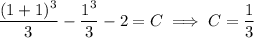
so that the solution to the IVP is

`F(x,y)=\frac{(x+y)^3}3-\frac{y^3}3-2y=\frac13`

`\implies\boxed{(x+y)^3-y^3-6y=1}`