Answer:
The minimum area of the top surface of a slab of ice is 45.8 m²
Step-by-step explanation:
Given that,
Thickness = 0.30 m
Mass of car = 1100 kg
Density of water
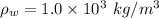
Density of ice
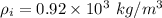
We need to calculate the minimum area of the top surface of a slab of ice
Using Buoyant force force
Total weight of car + ice weight = weight of water displaced
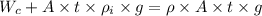
Put the value into the formula
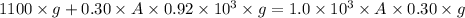
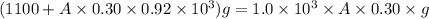
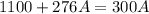
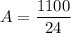
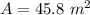
Hence, The minimum area of the top surface of a slab of ice is 45.8 m²