Question

I built a storage shed in the shape of a rectangular box on a square base. The material that I used for the base cost $4 per square foot, the material for the roof cost $2 per square foot, and the material for the sides cost $2.50 per square foot; and I spent $450 altogether on material for the shed. What should the side of the base be in order to maximize the volume of the shed?

Answer 1

side of 6.124 ft and height of 3.674 ft

Explanation:

Let's s be the side of the square base and h be the height of the rectangular box.

The base and the roof would have an area of
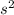`s^2` and cost of

`4s^2 + 2s^2 = 6s^2`

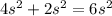
The sides would have an area of 4sh and cost of 4sh*2.5 = 10sh

So the total cost for the material is

`6s^2 + 10sh = 450`

`10sh = 450 - 6s^2`

`h = 45/s - 0.6s`

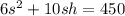
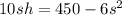
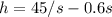
The volume of the shed has the following formula

`V = s^2h = s^2(45/s - 0.6s) = 45s - 0.6s^3`

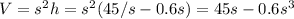
To find the maximum value for V, we can take its first derivative, and set it to 0

`(dV)/(ds) = 45 - 1.2s^2 = 0`

`1.2s^2 = 45`

`s^2 = 45 / 1.2 = 37.5`

`s = √(37.5) = 6.124 ft`

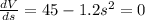
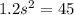
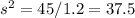
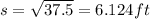
h = 45/s - 0.6s = 3.674 ft