Answer:
The answer to the given problem is given below.
Step-by-step explanation:
i. Should the money be invested?
If the money is invested there is a benefit of $150 x 6 + 50 x 5 = $1150. Since this is larger than $950, the money should be invested.
Assume now that the city is considering installing gates to charge tickets at a price of P per person for access to the park in order to repay the investment.
ii. Can the city Önance the investment by charging appropriate entrance fees.
Yes: if P = 5, 200 families will pay the price for a total revenue of $1000 > $950.
iii. What are all the prices P that are su¢ cient to repay the investment? Which one maximizes revenue?
If P > 5, only the 150 families who value the show at $6 will be willing to pay it. In this case the highest revenue would be obtained by charging $6 which only yields revenue of $900 < $950. So, no price P > 5 is sufficient to fund the investment. We saw above that P = 5 yields revenue equal to 1000. This is clearly the highest revenue that can be obtained. To find the lowest price that can be charged that is sufficient to recoup the cost, note that any P
 5 would lead to 200 people willing to pay the price. Thus revenue for such prices is 200P.
5 would lead to 200 people willing to pay the price. Thus revenue for such prices is 200P.
Set 200P = 950, Solution is:
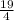 .
.
(iv) Which if any of the prices you found in (iii) lead to the suffocient outcome.
Any price such that
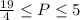 leads to the efficient outcome because at these prices all consumers will be willing to buy.
leads to the efficient outcome because at these prices all consumers will be willing to buy.
Assume now that there are 10,000 additional families who are only willing to pay $1 for the show.
(v) How does this change your answers to parts (i), (ii), (iii), and (iv)?
Answer to (i) is unchanged: we now have even more people who value the good, so we definitely want to produce it. (ii) Yes. For instance, by charging $1 we get $10,200. (iii) In order to raise $950, we can still charge the prices we found in part (iii). In addition, if we charge P
 1 we get all the people who value the show at 1.
1 we get all the people who value the show at 1.
Such prices raise $10; 200P. Breakeven price is such that 10200P = 950, Solution is:
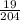 . Thus, any price such that
. Thus, any price such that
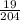
 P
P
 1,
1,
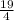
 P
P
 5 leads to enough money to repay investment. The price that maximizes revenue is $. 1
5 leads to enough money to repay investment. The price that maximizes revenue is $. 1
Part (iv): Only the prices such that
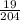
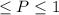 lead everybody to participate so only these are compatible with efficient allocation.
lead everybody to participate so only these are compatible with efficient allocation.