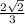Answer:
The answer to your question is e =
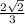
Explanation:
Data
Ellipse = 36x² + 4y² = 9
e = ?
Formula
e = c/a
Process
1.- Convert the equation of the ellipse to the canonical form
36x² + 4y² = 9
- Divide by 9 both sides
36/9x² + 4/9y² = 9/9
4x² + 4/9y² = 1
x² /(1/4) + y² / (9/4) = 1
b² = 1/4 b = 1/2
a² = 9/4 a = 3/2
2.- Find c
a² = b² + c²
c² = a² - b²
Substitution
c² = 9/4 - 1/4
Simplification
c² = 8/4
c² = 2
c=

3.- Find the eccentricity
e =
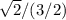
e =