Question

The acceleration of a particle as it moves along a straight line is given

bya=(2t-1)m/s2,where t is in seconds.If s=1m and v=2m/s when t=0, determine the particle’s velocity and position when t = 6s . Also determine the total distance the particle travels during this time period.

Answer 1

V_t=6 = 32 m/s

Step-by-step explanation:

The origin is at point 0 with the positive motion to the right

The instantaneous acceleration is change of velocity measured at infinitesimal interval of time, so the expression for instantaneous acceleration is:

a=dv/dt

From here we can express dv as:

dv = a dt

Replace a by 2t — 1

dv = (2t — 1) dt

Integrate both sides of equation

`\int\limits^v_a {2t-1} \, dv`

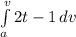
v=t

a=t_0

putting these value in integral

v-v_0=(t^2-t)-(t_0^2-t_0)

We know that v_0 = 2 at t_0 = 0, so we'll replace t_0 and v_0 by their values

v — 2 = (t^2 — t) — (0^2 — 0)

From here we can write the expression for v as:

v_t=6=6^2-6+2 (1)

So the velocity at t = 6 s is:

v_t=6 = 32 m/s

V_t=6 = 32 m/s

In order to determine the total distance travelled, we must check how maw times the particle has changed its direction, i.e. how many times its speed was equal to zero

To do that, we'll just replace v by 0 in expression (1)

0 = t^2 — t + 2

The roots of the quadratic equation are:

t_1/2=1± √(1^2-4*2*1)/2

Since 1^2-4*2*1 < 0, the quadratic equation have no real roots, so we can say that the velocity is always positive, i.e. to the right

Now that we have all the details, we can correctly draw the path of the particle

We can see from the sketch that the total distance traveled is:

s^T=Δs_0-1

s^T=| s_1 - s_0 |

Replace s_0 by its value

s^T=| s_1 - 1 | (2)

In order to determine the position of particle at t = 6 s, we'll need to determine the expression for s as function of time

Since we have already wrote expression for v as function of time (step 2), we'll use expression to get the expression for s

v= ds/dt

Multiply both sides of equation by dt

v dt = ds

Replace v by expression (1)

(t^2 — t + 2) dt = ds

Integrate both sides of equation

`\int\limits^t_b {x} \, dx`

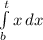
t=s

b=(s=0)

x=(t^2 — t + 2)

dx=ds

putting these value in integral

(t^3/3-t^2/2+t)-(t_0^3/3-t_0^2/2+t_0)= s-s_0

Since s = 1 m at t = 0, and we want to determine the position s at t = 6, we'll replace so by 1, t_0 by 0 and t by 6

(6^3/3-6^2/2+6)-(0^3/3-0^2/2+0)=s_t=6-1