Answer:
8418 ft lbf
Step-by-step explanation:
Let g = 32 ft/s2. The gravitational force that is parallel to the incline is
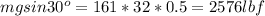
The normal force that acting on the block is the gravity force component that is perpendicular to the incline:
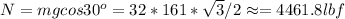
The friction force is the product of normal force and coefficient
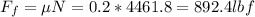
So the net force is force of gravity subtracted by friction force
F = 2576 - 892.4 = 1683.6 lbf
So the work by this force over 5 feet distance is
W = Fs = 1683.6*5 = 8418 ft lbf