1. C(x, y) = (7.3, –3.9)
2. C(x, y) = (17, –1.5)
Solution:
Question 1:
Let the points are A(3, –5) and B(19, –1).
C is the point that on the segment AB in the fraction
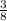 .
.
Point divides segment in the ratio formula:
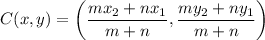
Here,
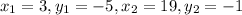 and m = 3, n = 8
and m = 3, n = 8
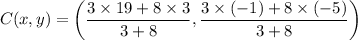
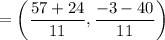
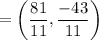
C(x, y) = (7.3, –3.9)
Question 2:
Let the points are A(3, –5) and B(19, –1).
C is the point that on the segment AB in the fraction
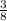 .
.
Point divides segment in the ratio formula:
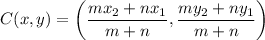
Here,
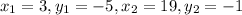 and m = 7, n = 1
and m = 7, n = 1
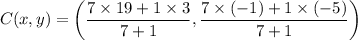
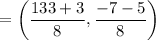
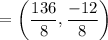
C(x, y) = (17, –1.5)