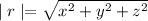Question

Object A has a position as a function of time given by A(t) = (3.00 m/s)t ˆı + (1.00 m/s2 )t2 ˆ. Object B has a position as a function of time given by B(t) = (4.00 m/s)t ˆı + (-1.00 m/s2 )t2 ˆ. All quantities are SI units. What is the distance between object A and object B at time t = 3.00 s?

Answer 1

18.25 units

Step-by-step explanation:

We are given that

The position of object A=
`A(t)=(3.00m/s)ti+(1.00m/s^2)t^2j`

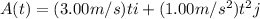
The position of object B=
`B(t)=(4.00m/s)ti+(-1.00m/s^2)t^2j`

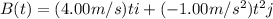
We have to find the distance between object A and object at time t=3.00 s

Substitute t=3 s

`A(3)=9i+9j`

`B(3)=12i-9j`

The distance between A and B

`A(3)-B(3)=9i+9j-12i+9j=-3i+18j`

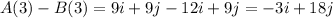
The magnitude of distance between A and B

`\mid r\mid=√((-3)^2+(18)^2)=18.25 units`

Using the formula magnitude of position vector

r=xi+yj+zk

`\mid r\mid=√(x^2+y^2+z^2)`