Answer:
Null hypothesis :
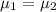
Alternative hypothesis:
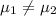
Or equivalently:
Null hypothesis :
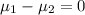
Alternative hypothesis:
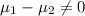
Other important thing is that on the alternative hypothesis we never can have the symbol equal.
Explanation:
Some previous concepts
A hypothesis is defined as "a speculation or theory based on insufficient evidence that lends itself to further testing and experimentation. With further testing, a hypothesis can usually be proven true or false".
The null hypothesis is defined as "a hypothesis that says there is no statistical significance between the two variables in the hypothesis. It is the hypothesis that the researcher is trying to disprove".
The alternative hypothesis is "just the inverse, or opposite, of the null hypothesis. It is the hypothesis that researcher is trying to prove".
On this case the she wants to proof if that she samples from will differ from her comparison population. So this needs to be on the alternative hypothesis. And the complement of the alternative hypothesis would be on the null hypothesis.
Solution to the problem
So then she needs to conduct a two tailed z test. Let's assume that the population 1 is the population of interest and the population 2 is the comparison population so then the systam of hypothesis are:
Null hypothesis :
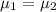
Alternative hypothesis:
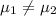
Or equivalently:
Null hypothesis :
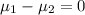
Alternative hypothesis:
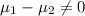
Other important thing is that on the alternative hypothesis we never can have the symbol equal.