Answer:
The answer to the question is
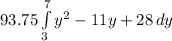 = 250 lb force
= 250 lb force
Step-by-step explanation:
The given variables are
Height of triangular plate = 4 ft
Base of triangular plate = 6 ft
The hydro-static force on the triangle is the product of pressure at a particular depth and the area of the surface of the triangle at that depth
the width of the triangle is given by
slope =
Here we have y = -4/3x +4 and the depth from the top at any y is 7 -y
Therefore pressure = 62.5×(7-y)
And the area of a strip is is given by 2 times the x coordinate and Δy
That is area =
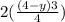 ×Δy
×Δy
Force on a strip is given by Force = Pressure × Area
= 62.5×(7-y)×
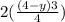 ×Δy Which gives 93.75 ×(7-y)(4-y)Δy
×Δy Which gives 93.75 ×(7-y)(4-y)Δy
Hence hydrostatic force =
 =
=
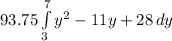
=
![93.75[{(y^3)/(3) -11(y^2)/(2) +28y} ]\limits^7_3](https://img.qammunity.org/2021/formulas/physics/high-school/v45fk7nskbuscg39cobaa6ekfe2x5vqpxg.png) = 250 lb force
= 250 lb force