Option A:
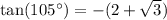
Solution:
To evaluate tan(105)°:
105° can be written as sum of 60° and 45°.
tan(105)° = tan(45 + 60)°
Using the summation identity:
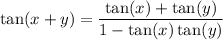
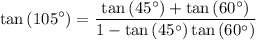
We know that, tan(45)° = 1 and tan(60)° = √3
Substitute this in the above equation.
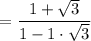
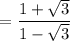
To rationalize the denominator multiply by the conjugate
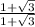 .
.
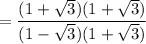
Using exponent formula:
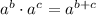 and
and
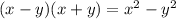
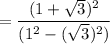
Using exponent formula:
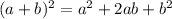
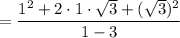
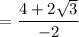
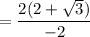
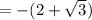
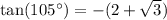
Hence option A is the correct answer.